Fast differentiable operations on arbitrary-dimensional floating-point arrays

The paper’s name is “What Operations can be Performed Directly on Compressed Arrays, and with What Error?” and you can read it here: https://dl.acm.org/doi/10.1145/3624062.3625122.

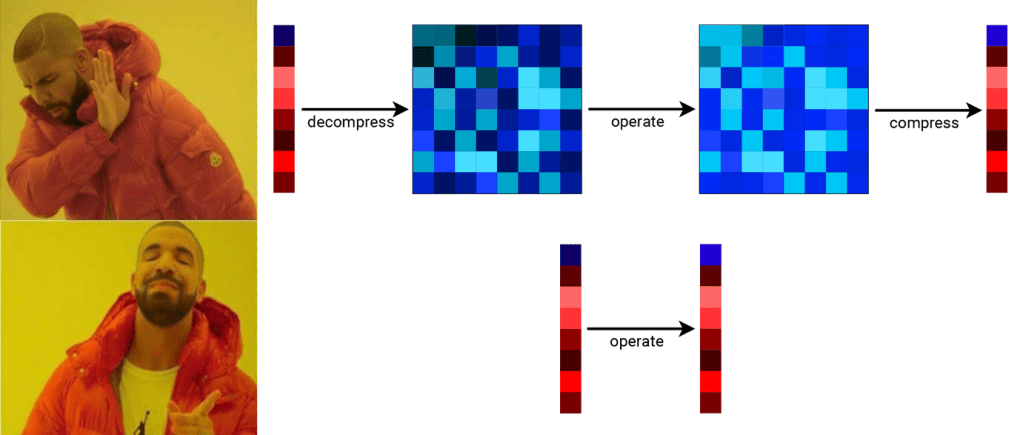
The main idea is that we’ve designed a compression method called PyBlaz that allows you to transform arbitrary-dimensional floating-point arrays (often called tensors) in certain ways without decompressing them. These transformations include negation, addition, mean, variance, L2 norm, and structural similarity index measure, all in at most logarithmic time with sufficient threads. It’s important to note that there’s no matrix multiplication and no element-wise multiplication (Hadamard product), so I’d like to urge you to not try to stick PyBlaz where it doesn’t belong.

This actually started because I was investigating its predecessor Blaz (https://arxiv.org/abs/2202.13007), and implementing it myself in order to understand it better. I wasn’t trying to make anything new; I was just implementing it in ways that I considered good practice, which included not limiting it to 2 dimensions and also taking advantage of GPUs if possible, which was natural to do in PyTorch. I also removed one of the steps in Blaz (called normalization in their paper) to facilitate those additional transformations involving the dot product.

So, eventually this was published in the 9th International Workshop on Data Analysis and Reduction for Big Scientific Data and was awarded Best Paper in the workshop.